Здесь описано некое универсальное средство для решения любых задач по физике (алгоритм). В первой части статьи даны несколько общих определений и утверждений, необходимых для понимания вопроса. Во второй части приводятся рассуждения, связывающие эти общие понятия с практикой действий при обучении решению задач. В заключение приводится разбор нескольких решения задач с необходимыми комментариями.
Для начала, как водится, несколько определений.
Понятие «задача. М.Я. Басов (1892—1931) отмечал, что для самых разнообразных учебных и жизненных ситуаций общим является момент задачи как таковой. Этот общий момент (проблема) связан с необходимостью для человека открыть то, чего он еще не знает и что нельзя просто увидеть в предмете; для этого ему потребуется определенное действие с этим предметом.
Проблемная ситуация, по Л.М. Фридману, – это не просто затруднение, преграда в деятельности субъекта, а осознанное субъектом затруднение, способ устранения которого он желает найти. Значит, задача есть модель ситуации, элементом которой является субъект, осознавший затруднение в своей деятельности.
Учебная задача — стоящая перед обучаемым цель, которую надлежит ему выполнить в определенных условиях. Особенность учебной задачи состоит в том, что при ее решении учащийся должен найти общий способ (принцип) подхода ко многим конкретно-частным задачам определенного класса. Главным методом обучения должен стать метод введения учащихся в ситуацию учебной задачи и организации учебных действий. Учебная задача решается посредством системы учебных действий. Первым из них является преобразование проблемной ситуации, входящей в такую задачу. Это действие нацелено на поиск такого исходного отношения предметных условий ситуации, которое служит общей основой последующего решения всего многообразия частных задач. Другие учебные действия позволяют учащимся моделировать и изучать это исходное отношение, выделять его в частных условиях, контролировать и оценивать процесс решения учебной задачи. Без субъекта нет задачи. То, что для одних является задачей, для других может ею не быть. Другими словами, не всякий текст, содержащий вопрос (требование) является задачей для данного субъекта.
Состав задачи как данное и искомое, известное и неизвестное, условие и требование (вопрос задачи) представляется в форме исходного и будущего как результата разрешения отношения между компонентами состава задачи. Задача рассматривается как сложная система информации о каком-либо явлении, объекте, процессе, в котором четко определена лишь часть сведений, а остальная неизвестна. Она может быть найдена лишь на основе решения задачи или сведений, сформулированных таким образом, что между отдельными понятиями, имеются несогласованность, противоречие, требующие поиска новых знаний, доказательства, преобразования, согласования.
В трактовке Л. М. Фридмана любая задача состоит из одних и тех же частей:
1) предметная область —класс фиксированных обозначенных объектов, о которых идет речь;
2) отношения, которые связывают эти объекты;
3) требование задачи —указание о цели решения задачи, то, что необходимо установить в ходе решения;
4) оператор задачи —совокупность тех действий, которые надо произвести над условием задачи, чтобы выполнить ее решение.
Способом решения задачи называется всякая процедура, которая при ее осуществлении решателем может обеспечить решение данной задачи.
Методика обучения решению задач предполагает выделение спектра умений решать задачи. Первый этап составляют действия: выделение условия и требования задачи, объектов и отношений между ними, выполнение рисунка, отметка на нем данных и искомых элементов, краткая запись условия и заключения задачи. Содержание этого этапа решения, как правило, реализуется на практике. Второй этап включает в себя анализ условия и требования задачи. Под анализом условия задачи будем понимать выявление такой информации, которая непосредственно не задана условием, но присуща ему. Анализ требования задачи предполагает выяснение возможных путей ответа на вопрос задачи.
Важнейшим компонентом умения анализировать требование задачи является умение преобразовывать требование задачи в равносильное ему. Проблема формирования этого умения непосредственно связана с вооружением учащихся как можно большим числом признаков и свойств понятий. Выполнение анализа требования задачи предполагает наличие ассоциаций: осознание термина, обозначающего понятие, – осознание определения этого понятия и термина, обозначающего понятие, – осознание его характеристических свойств. Важными компонентами анализа требования задач является умение составлять вспомогательные задачи (подзадачи), и умение видеть различные пути решения задачи.
Следующий этап – осуществление плана решения. Решение задачи, как правило, заканчивается получением ответа или, в лучшем случае, обсуждением базиса и идеи решения.
Особое значение имеет четвертый этап – взгляд назад. Его особенность обусловлена тем, что он является хорошим полигоном для развития творческой инициативы учащихся, самостоятельности их мышления. Несмотря на большие возможности этого этапа в развитии ученика, он почти не используется учителями на практике.
* * *
Уф! Так-то это так, а пользы учителю в повседневной работе от этого немного. Попробуем из этой информации извлечь практический интерес: понять, как научить ученика решать задачи по физике. Правда быстро не получится. Потребуется немного потеоретизировать, точнее поразбираться, потолковать, чтобы понять, чему следует учить.
А что мы обычно делаем для решения задачи? Используя данные в условии задачи, мы преобразуем это условие в более удобное для нас - подбираем модель процесса (последовательности процессов), происходящих в задаче.
Нет, даже не так, а по-простому. Формула (закон, график, таблица и пр. модели) в учебной задаче подбирается нами из фонда наших знаний о физике. При решении же научной задачи эту модель мы вынуждены создавать заново в процессе научной деятельности, что само по себе уже может составлять научный продукт, дополнительный к решению задачи. Подставляя в эту формулу данные из условия, мы получаем ответ (решение задачи).
Из этого мы сделаем два важных вывода.
Первое, для решения задач надо научиться подбирать модели из запаса готовых, проще говоря, знать физику. При этом не просто знать, не просто уметь рассказывать о таком-то явлении, а знать в том числе его основные признаки и свойства, по которым мы можем его узнать (обнаружить) в условии задачи и какими формулами (законами, уравнениями, графиками) оно описывается (законы протекания явления). Это сложнейшее для ученика умение, над которым следует упорно и целенаправленно работать. Это утверждение тем более важно, что на такую работу нас обычно ничего не наталкивает. Изучая явление, мы попутно должны изучать, как его узнать (обнаружить в условии задачи). Наличие скорости – это наличие кинетической энергии, наличие высоты – наличие потенциальной энергии тяготения, наличие деформации – наличие потенциальной энергии упругой деформации. Наличие неуравновешенной силы – наличие либо ускорения, и/или деформации. Отсутствие силы – состояние покоя или равномерного прямолинейного движения. И так во всем! Целенаправленно давать учебную информацию применительно к будущему решению задач!
Поскольку явлений, изучаемых в школьной физике много, а их признаков еще больше, и обращаться к ним мы вынуждены часто, полезно сформулировать их кратко, даже афористично, а может и графично (см. шаталовские опоры). Тогда запомнить их, а главное вспомнить в нужный момент будет гораздо легче. Также важно обращаться к ним каждый раз с одними и теми же словами, одними и теми же формулировками!
Важное примечание. Знание - сила, если они есть. А если их нет, или пусть даже есть, но кургузые, неполные, приблизительные. Тогда это полностью выбивает ученика из учебного процесса! Мы можем делать вид, что мы учим, а дети могут делать вид, что они учатся, но ситуация полностью тупиковая! Однако есть простой способ педагогически правильно решающий этот образовательный парадокс. Справочник (!), который мы разрешаем использовать на некоторых уроках, где ученик может сам найти нужный арсенал формул, и самостоятельно из этого арсенала выбрать нужную формулу (см. пример правильного справочника: http://sverh-zadacha.ucoz.ru/lessons/lessons.html). Многие дети и сами начинают вести на последней странице тетради сводку формул, но, ничего не запрещая, мы настоятельно рекомендуем пользоваться нашим, проверенным, полным, идеальным справочником.
Второе, подобрав формулы, необходимо умение сделать выбор плана решения. Так, поняв, что в задаче необходимо воспользоваться формулой работы, выбираем одну из возможных примерно девяти, изучаемых в школе. Такой выбор тоже не простая вещь, учитывая, что решение более или менее внятной задачи, как правило, не ограничивается одним действием. А значит нам предстоит действовать в условиях неочевидности, когда ученику далеко не всегда ясны дальнейшие пути решения задачи.
Конечно, для решения задач необходимы и специальные знания, относящиеся к умению решать задачи (знание приемов, способов), но это дело наживное, как говорится в процессе.
Подведем первый итог. Чтобы научить решать задачи, среди прочего, что мы обычно делаем, на уроках изложения нового материала необходимо заранее давать так теорию, чтобы в ней среди прочего был ясный акцент на признаки опознавания изучаемого явления с прицелом на решение задач. Таким образом решение задач не является самостоятельным элементом учебного процесса, а должно быть органично вплетено в его ткань.
На уроках решения задач ученикам необходимо иметь справочники по физике с целью создания ситуации полноты правильных и точных знаний.
На этих уроках необходимо, в том числе обучать выбору формул из набора, а также смелости действия в условиях неочевидности (смелости начать действовать вслепую с верой в силу алгоритма решения задач).
Обращаем ваше внимание, что это совсем не то, о чем мы обычно думаем перед уроком решения задач и не то, о чем нам говорят методисты! А о чем они говорят? Как правило, показывают нам, как решить ту или иную задачу. И всё! И мы, думая, что учим ученика решать задачи, действуем точно так же. Не обучая ничему, кроме одного, повторять за нами решения уже кем-то решенных задач. Я даже думаю, что есть немало учителей физики, которые за свою жизнь не решили сами ни одной задачи. Ибо сказано выше: задача должна открыть то, чего субъект еще не знает и что нельзя просто увидеть в предмете. Иначе задачи просто нет.
Мы увлеклись. Опять грешим общими рассуждениями. Пора перейти к конкретике, помня, конечно, о том, что мы сказали выше.
* * *
Для обучения решению задач мы используем специальные уроки решения задач, заложенные в годовом планировании курса физики. Понятно, что взять наугад три-четыре первые попавшиеся задачи из дидактического материала и просто показать, как выполняется их решение, никуда не годится. Отбор задач для такого урока важнейшее условие нашего успеха.
Первый такой урок мы проводим в 7 классе по теме «Плотность вещества».
Предлагаем вам для такого урока следующие задачи (из задачника В.И. Лукашика [7]).
1. Кусок металла массой 461,5 г имеет объем 65 см3. Что это за металл?
2. Картофелина массой 59 г имеет объем 50 см3. Определите плотность картофеля.
3. Какова масса чугунной гири объемом 143 см3?
4. Какого объема (в литрах) следует взять ведро, чтобы в него поместилось 10 кг воды?
5. Какой длины надо взять медную проволоку сечением 5 мм2, чтобы она имела массу 20 г?
6. Чугунный шар при объеме 125 см3 имеет массу 800 г. Сплошной этот шар или полый?
Прежде чем читать дальше, попробуйте ответить на вопрос, какую задачу из выше приведенных вы бы выбрали в качестве первой для урока решения задач?
А надо вот какую! Этот выбор должен определяться не тем, что нам нравится, а поставленной учителем перед собой задачей. Что для нас важно? Чему мы хотим научить в первую очередь?
Во-первых, мы с самого начала должны научить детей правильно оформлять решение задачи. Во-вторых, мы должны научить рассуждать и действовать ученика определенным образом во время решения им расчетных задач по физике.
Для этого лучше других подойдет задача №2. Она содержит наименьшее количество избыточных для детей усложнений и позволяет в наиболее «чистом» виде достичь наших целей.
Если вам захотелось в качестве первой разобрать что-нибудь типа задач № 5 или № 6, то вы не правы. Авторитетно утверждаю, разбор этих задач ничему не научит ваших учеников.
Есть не мало учителей, которые не учат учеников. Они требуют, чтобы ученики сами учились, если захотят и если смогут. А если не смогут? Тогда они не достойны того, чтобы мы на них тратили время! О, как!
А вы сможете наизусть прочитать тысячу стихов без подготовки? Я любитель стихов, я, наверное, смогу и больше, не считал. А вы сможете? У нас школа с гуманитарным уклоном. Как девчонки поют на три, а то и четыре голоса, но я так не смогу никогда! Тогда по какому праву мы хотим требовать от учеников невозможного, да еще и одариваем их за неспособность своим презрением! Требовательность это хорошо, но это не есть требовательность. Ничего учительского за этим не стоит. Только высокомерие и гордыня.
А ты научи ученика, тогда ты Учитель!
Итак, про картофелину.
Задача 1. Картофелина массой 59 г имеет объем 50 см3. Определите плотность картофеля.
Первое, что мы делаем при решении любой задачи, выделяем ключевые слова/понятия (чаще всего это набор физических величин), в нашем случае это масса, объем и плотность. Последнее самое главное слово в задаче, оно входит в вопрос задачи, является нашей конечной целью.
Второе, какой закон (формула, уравнение, соотношение) связывает эти величины между собой? Это формула плотности: ρ = m/V.
Третье. Анализируя это соотношение, видим, что оно сразу решит нашу задачу и даст ответ. В более сложных задачах этот алгоритм будет иметь продолжение, но пока для ребенка достаточно.
Четвертое. Учим, как принято в физике оформлять решение задачи.
Показываем как принято кратко записывать условие задачи, как работают с системой единиц, как записывают нужные формулы, как подставляют данные и получают ответ.
Дано:
m = 59 г
V = 50 см3 |
ρ = m/V;
ρ = 59 г/50 см3= 1,18 г/см3
Ответ: ρ = 1,18 г/см3 |
| ρ - ? |
Обращаем внимание учеников на отличие от привычной для них записей на уроках математики.
Не правильно: m - 59 г, m = 59 гр. Не правильно: ρ = ?
Не правильно писать: p, или Р, или как-то иначе. Правильно: ρ.
Пятое. Анализируем полученный результат (ответ). На сколько это правдоподобный ответ? К чему близко численное значение плотности картофеля? К плотности воды! Не случайно, ведь картофель содержит примерно 75% воды. Обсуждения ответов к задачам важнее численного результата. Они «овеществляют» результат, наполняют его смыслом, позволяют отличить правдоподобный ответ от неправдоподобного.
Здесь мы показываем, как надо рассуждать при решении задачи, чтобы от чтения условия дойти до получения ответа. Повторяя наши рассуждения, дети в дальнейшем должны научиться рассуждать аналогичным способом, решая задачи по физике. В пределе должны научиться решать задачи, которые они никогда не решали (решения которых им никто никогда не показывал). А вы их учите решать только те задачи, которые им показывали, и все?
Не слишком ли это мало для ученика? Так не вырастишь пытливый и самостоятельный ум!
Правда и то, что одно «показываем» само по себе слишком мало чему научит. К нему добавляем две неотвратимые вещи: домашнее задание и опрос на следующем уроке. А также всю совокупность последующих уроков, где будет решение задач. Вот тогда это будет учить!
Задача2. Кусок металла массой 461,5 г имеет объем 65 см3. Что это за металл?
Эта задача мало отличается от предыдущей, вот только в ней ответ неочевиден. Что искать? Мы-то понимаем - плотность, но для многих детей это не очевидно. Как масса и объем смогут указать на… вещество? Не просто! Не сообразят, посоветуйте действовать вслепую. А что мы в физике умеем? – Находить плотность вещества! Найдем, а там видно будет.
Разбирая эту задачу, мы уже стараемся, чтобы дети сами начали рассуждать в нашем стиле, строго следя за тем, чтобы они не сваливались на бытовизм. Продолжаем разучивать алгоритм…
Задача 3. Какова масса чугунной гири объемом 143 см3?
Это задание знакомит учеников с очень важными в физике способами решения обратных задач (см. эрдниевскую УДЕ). Ключевое понятие – масса. Как связаны между собой масса и объём? Мы знаем только одно: ρ = m/V, где плотность всегда можно узнать из таблиц. Но это не дает нам найти сразу массу. Некоторые учителя дают не одну формулу плотности, а еще и два следствия из нее: m = ρV и V = m/ρ. Тогда нет проблем в выборе решения. Но упрощая решение, мы выносим за скобки навык преобразования математических выражений, что будет важно в решении других, более сложных задач, а кроме того увеличивает объем информации для запоминания в три раза. Мы считаем навык много полезнее знания. А наш опыт показывает обучить преобразованию формул можно даже слабого ученика. В конце концов есть и более простой способ: в формулу плотности подставить числа и решить полученное уравнение относительно неизвестной массы. Мы показываем разные способы получения результата, пусть ученик сам выберет для себя то, что ему удобнее.
Дано:
ρ = 7 г/см3
V = 143 см3 |
ρ = m/V
Алгебраически. Домножим обе части равенства на V:
V ρ = m V /V
Сократим справа объем и поменяем правую и левую части равенства местами:
m = ρV = 7 г/см3 ·143 см3 = 1001 г.
Или арифметически (если с алгеброй сложности). Подставим известные величины в формулу ρ = m/V:
7 г/см3 = m/ 143 см3; чтобы найти делимое надо частное умножить на делитель:
m = 7 г/см3 ·143 см3 = 1001 г (сократив на см3).
Ответ: m = 1001 г |
| m - ? |
Все слова, а не только формулы, написанные нами в решении первых задач, ученики должны записать у себя в тетради в точно таком же виде! Слова важнее решений! В дальнейшем, однако, довольно часто мы будем их опускать, кроме специальных случаев.
Под конец урока полезно будет показать решение задачи в несколько действий.
Задача 4. Какой длины надо взять медную проволоку площадью сечения 5 мм2, чтобы она имела массу 20 г?
У ученика возникает вопрос, причем здесь длина L? С чем в нашей единственной пока формуле может быть связана длина? Только с объёмом: V = LS. Значит, искать будем объем! А зная его, найдем длину. Это называется преобразованием задачи в равносильную ей (см. начало статьи). Оказывается, вместо длины L нам следует искать объем V! А там уж дело сладится.
Обратили внимание? Мы решаем задачу (нащупываем план решения) до того, как сделали краткую запись условия задачи. В более сложных задачах мы будем действовать наоборот, краткая запись будет помогать в решении задач.
Дано:
ρ = 8,9 г/см3
S = 5 мм = 0,05 см2
m = 20 г |
V = LS.
Поделим обе части на S:
V/S = LS/S; сократим в правой части на S:
L = V/S.
Все бы хорошо, но V неизвестно, однако мы знаем другое:
ρ = m/V
Домножим обе части равенства на V:
V ρ = m V /V
Сократим справа на V:
ρV = m; поделим обе части на ρ, а затем сократим его в левой части:
V = m/ρ.
Теперь подставим это равенство в формулу длины:
L = V/S = m/(ρ·S).
Здесь известны все величины и уже можно найти ответ:
L = 20 г/(8,9 г/см3·0,05 см2) = 45 см. (Сократив на г и на см2).
Можно решать задачу и по частям: найдем численное значение объема, потом и длину найти сможем.
Ответ: L = 45 см. |
L - ? |
Объясняем каждую задачу, не торопясь, пока не почувствуем, что мы находим понимание в классе. В заключение записываем в тетрадях алгоритм действий при решении количественных задач.
1. Читаем внимательно условие задачи, стараясь понять что происходит по условию задачи. Выделяем ключевые слова в условии, главное из которых содержится в вопросе задачи.
2. Для главного ключевого слова (физической величины) находим формулы (можно и из справочника).
3. Из всех формул выбираем такую, которая связывает максимальным образом главную величину (вопрос задачи) и остальные, упомянутые в условии задачи.
4. Анализируем ее на возможность найти решение задачи. Если в ней содержатся другие неизвестные, не позволяющие сразу найти ответ в задаче, проделываем пункты 2,3 и 4 для новой неизвестной величины. Действуем так, пока не останется неизвестных величин.
5. Собираем все найденные формулы в одну и находим ответ. Можно решать задачу и по частям.
6. Анализируем ответ на предмет его правдоподобия. |
Или графически:
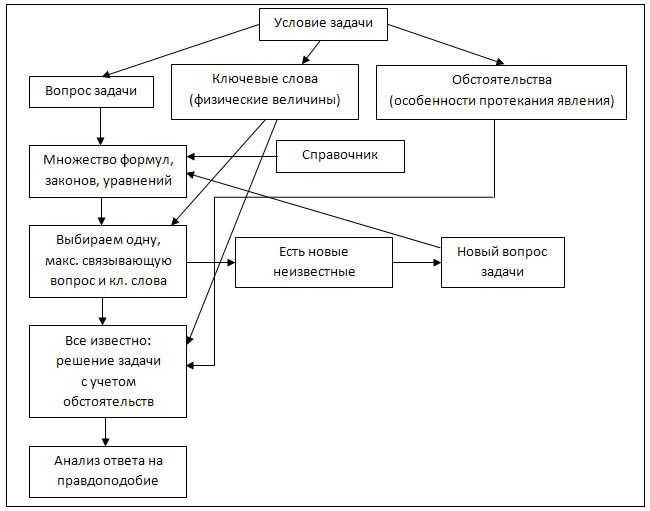
Мы считаем нужным предлагать и текстовую и графическую версию алгоритма. Пусть сами выбирают, какая из них удобнее. Визуалы выберут графическую, гуманитарии – текстовую, аудиалы будут начитывать себе вслух текстовую, левополушарники графическую будут содержательно подкреплять текстовой. Вот и ладно!
Схема сложновата на первый взгляд, старайтесь избегать такого в младших классах, но в ней наглядно видно:
- из условия мы должны выделить три составляющие (вопрос, физические величины /данные/, обстоятельства, в которых протекает явление), а не один только вопрос. Краткая запись условия задачи – важная часть ее решения не являет нам все обстоятельства, без учета которых задача может быть решена не верно;
- на какой стадии решения задачи, какими средствами мы пользуемся, на что переносим свое внимание (где данные из условия, где справочник, где надо суметь сформулировать новый вопрос и т.д. Перенос внимания – еще одна большая трудность для ученика.)
- цикличность (одинаковость порядка действий вне зависимости от того, что надо найти).
Мы не заставляем заучивать алгоритм, но держать его перед собой обязательно. С ним ученик сможет решить гораздо больше задач, чем без него. Как только ученики становятся в тупик, мы тут же говорим: «А что нам подсказывает алгоритм?»
И какое домашнее задание вы задали бы в конце такого урока? Что следует спрашивать на следующем уроке? Это всегда зависит от того, что мы хотели достичь на уроке, но не достигли! Дома будет продолжение урока. И главный принцип – посильность для… троечника. Если вы хотите дать на дом решать аналогичные задачи для закрепления пройденного в классе, то это можно сделать только в очень сильном классе, и то это будет не самое полезное задание. Можно научить плавать человека, если его бросить в воду, желание выжить научит его быстро! Но так он научится плавать скорее всего только по-собачьи. А плавать красиво и быстро учат специальными приемами!
Надо сказать, что мы только еще первый раз показали, как решают задачи на физике и как следует рассуждать при решении и простых, и более сложных задач. И всё. Разве мы можем считать, что мы чему-то уже научили? Нет! Мы только показали, а нам надо, чтобы дети научились делать как мы (а потом и лучше нас). Значит, самое полезное дать ученикам заучить данные нами образцы решений по записям в их тетрадях. Заучить и оформление задач, и РАССУЖДЕНИЯ.
Следующий урок начинаем, как обычно, с проверки домашнего задания.
Что мы задавали? - Выучить!
Для чего? – Ну, не для того, чтобы «ущучить» нерадивых, а чтобы получилось решать. Потому пока не очень важно, все ли добросовестно выучили. Важнее проверить, умеют ли они рассуждать и оформлять свои рассуждения. А заодно и помочь доучить, что выучилось плохо. Поэтому сначала просим за 10 мин на листочке написать решения задач с прошлого урока. И тут мы не всё проверяем, а только запись решения! Рассуждения же спрашиваем у доски поэлементно, каждый по чуть-чуть, один вслед за другим, чтобы задействовать и опросить наибольшее количество учеников. Как у Е.В.Яновицкой («Великая дидактика без домашних заданий» (http://sverh-zadacha.ucoz.ru/Yanovitskaya.doc)). Для этого выводим на экран условия домашних задач с помощью проектора (на интерактивной доске), с помощью бумажного плаката или с заранее заготовленного текста домашних задач на боковой доске, а ученики демонстрируют письменно на доске и вслух выученные рассуждения, поэлементно решая задачу за задачей. В слабом классе начинаем в первой задачи, там же не тратим время на разбор четвертой задачи. В сильном - сразу задача 3. Записать краткое условие задачи, записать формулу плотности, вывести из нее формулу массы, правильно подставить данные из условия, получить и записать правильный ответ, проанализировать его.
Помогаем ученикам справиться, так чтобы быстро провести этот этап урока.
Не стесняемся вызывать несильных учеников для выполнения самых простых первых этапов. Это держит в материале слабых, а также дает им понять (пусть и иногда с помощью учителя), что все может получаться.
Самый жесткий контроль мелочей. Как называется величина, как обозначается плотность, как правильно пишется «ро» и пр. и пр. Ученик должен понять, здесь нельзя кое-как.
Заставляем не столько писать решение, сколько говорить, говорить. Говори вслед за мной, говори, как я…
Далее, если ученику мы показали образцовые действия при решении задач, если он их более-менее запомнил, мы это проверили, теперь последнее: решение аналогичных задач. Последние 25 мин урока наши ученики решают задачи из дидактического материала по индивидуальным карточкам. Не контрольная работа, поэтому мы бегаем по классу и говорим, говорим с нашими учениками о задачах, понуждая их действовать и рассуждать по нашему алгоритму, а не вопреки ему. При проверке этой самостоятельной работы – опять самый жесткий контроль мелочей. Они важнее сейчас, чем правильное решение задачи!
На дом задаем две - три аналогичные задачи, к ним обязательно добавим задание типа: придумать самому задачу на плотность вещества и представить ее решение. Ничто сильному ученику не позволяет во всей полноте постичь специфику темы, как сочинение условий задач и их решение! Например, ученик придумал задачу: "Брусок массой 200 г имеет объем 1 см3. Найти плотность вещества." С виду простая задача, ан нет! Что это за вещество, плотность которого 200 г/см3? Не бывает! Так не годится. Значит, чтобы составить задачу, надо было сначала решить обратную, по заданной плотности найти объем, а затем уже составить задачу!
Мы не требуем, чтобы каждый ученик решил дома все задачи, а то спровоцируем повальное списывание.
Заучивание задач (обыкновенная зубрежка) – это очень важно. Оно приучает вникать в решение задачи, сделать невозможным поверхностное отношение. Образцы (си речь, идеальные решения) исключают разброд и шатание. Также важно и заучивание формул. Но не как отдельное учебное действие непонятное для чего. Знание формул требуется здесь в явном и неотвратимом виде. Ведь мы заучиваем не просто отдельные формулы, а вместе с условиями их применения, когда заучиваем образец решения задачи.
Наша работа напоминает обучение рисованию в хорошей художественной школе. Там один из приемов обучения рисованию – копирование полотен великих. Вместе с копированием образцов мастеров рисунка ребенок впитывает сам дух процесса рисования, нечто такое, что не объяснишь, не покажешь и не расскажешь. Нечто проникающее в нас помимо воли и сознания, иными путями, чем через обычные наши пять чувств! Великий Бенуа тщательнейшим образом копировал Малевича, чтобы понять новое для него искусство футуристов, которое он не принимал и оно не приняло его!
Зубрежка!.. А как же творчество?!
Всему в этом мире должно быть дано своё место. Без одного немыслимо другое. Сперва зубрежка, тренинги, тогда появляется настоящие возможности для подлинного творчества. Либо ты будешь учить плавать детей быстро, красиво, технично, либо они будут плавать «творчески».
Научив ребенка решать задачи на плотность вещества, мы вместе с тем добились гораздо большего. Мы дали ему некое универсальное средство для решения любых задач по физике!
Мы всегда проделываем работы больше, чем это обычно требуется. Потому что мы ставим перед собой большие задачи: дать универсальное средство для решения большего спектра задач по физике, чем требует школьная программа, реальное обучение троечников, обеспечение поступления в технический вуз, безпроблемное обучение физике затем в вузе и т.д.
А фокус вот еще в чем. Наш алгоритм универсален, он годится для любого типа задач и потому нам не приходится для каждого нового типа задач начинать обучение заново! Ребенку проще иметь в голове нечто одно универсальное, чем помнить как решаются все типы задач, что изучаются в школе.
Второе, алгоритм минимизирован. В нем содержится именно то и только то, что надо уметь делать для решения задач.
Некоторым покажется то, что мы делали выше, только отягощает. Ведь на самом деле всё это можно делать гораздо проще, и нечего огород городить! Однако, мы приведем ещё два примера, где попробуем показать нужность всего этого там, где задачи становятся сложнее, а решить их нам помогает всё тот же, но уже привычный для детей алгоритм. Если вы, что называется, в теме, то не трудно будет увидеть, задачи сложнее, а решать их ребенку так же просто, как раньше.
Приведем примеры того, как мы обучаем детей приёмам решения более сложных задач.
Задание из ГИА (9 кл.) Электрический нагреватель за 20 мин доводит до кипения 2,2 кг воды, начальная температура которой 10 °С. Сила тока в нагревателе 7 А, КПД нагревателя равен 45%. Чему равно напряжение в электрической сети?
Приведем для сравнения решение, данное авторами задачи.
Решение
КПД нагревателя — есть отношение теплоты Q1, поглощённой водой к теплоте Q2, выделившейся на нагревателе за то же время:
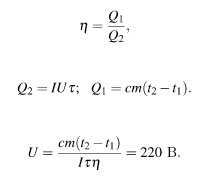
Ответ: 220 В
Решение ясное, придраться не к чему, кроме орфографии: тире перед «есть» не ставится. Но мы убеждены, дайте решение ученикам в таком виде и он аналогичную задачу не решит. Такое решение ничему не учит. Здесь опущена важная часть рассуждений, которую мы покажем ниже.
Согласимся, сильный ученик со временем сам освоит недостающие рассуждения. Но, во-первых, со временем, во-вторых, только сильный.
Итак. Задачи на КПД решаются с помощью одного приёма. Встретив слово «КПД» или «пошло столько-то процентов», наш ученик сразу пишет (вслепую, не обращая внимание на то, что нужно найти, что дано и пр.): η = Qполезн/Qзатрач .
Примечание. Мы пишем в индексе длинно «полезн.», а не более краткое «пол.» Последнее легко спутать со словом «полное» или какими-либо другими.
Еще примечание. Наши ученики привыкают смело приступать к решению задач, не имея четкого плана, не видя решение задачи до конца, вслепую, или как мы это называем умение действовать в условиях неочевидности. Они верят, что, если следовать определенным формальным процедурам, то план решения скорее всего сам нарисуется. Если есть лабиринт, то и есть из него выход!
Далее, как мы говорим, с учетом обстоятельств задачи определить, что есть полезное тепло и что есть затраченное. По условию задачи:
- польза здесь состоит в нагревании воды, тогда: Qполезн = cm(t2 – t1);
- затрачивают для этого электроэнергию, значит: Qзатрач = IUτ.
(Из трех формул для закона Джоуля-Ленца выбираем ту, в которой содержится наше неизвестное U и наибольшее количество данных из условия задачи).
Подставляем эти соотношения в формулу КПД. Теперь только начинаем решать задачу! Анализируем, все ли нам известно, и после алгебраических преобразований получаем ответ.
Следовательно, план решения задачи таков:
- пишем формулу КПД;
- определяем формулы для полезного и затраченного тепла, исходя из условия задачи;
- подставляем найденные соотношения в формулу КПД;
- анализируем, все ли дано в полученной итоговой формуле (кроме неизвестного U);
- с помощью алгебраических преобразований выводим соотношение для неизвестного;
- подставляем данные из условия задачи (следя за системой единиц) и получаем ответ.
Теперь ясно, что должен знать и уметь наш ученик:
1. Знать прем для решения задач на КПД, знать формулу КПД.
2. Уметь по условию задачи определять, что есть полезная энергия, а что есть затраченная энергия. Знать формулы энергии, работы, мощности, теплоты. Уметь выбирать из них те, что подходят по смыслу задачи.
3. Уметь соотнести итоговую формулу и данные задачи, чтобы определить, решаема ли задача на этом этапе, или понадобятся дополнительные действия для получения ответа. Это простой навык. Одно неизвестное – решаема, более одного неизвестного - пока решить не удастся.
4. Уметь производить алгебраические преобразования, чтобы выразить неизвестное через известные.
5. Иметь навык арифметических вычислений, иметь навык работать с системами единиц.
Примечание. Допустимо без снижения оценки вместо алгебраических преобразований решать задачу по частям, если кому-то и в 9 классе трудно с алгеброй. Найти Qполезн, подставить в формулу значение КПД, значение Qполезн, под дробью два известных Iτ, умноженные на U. Решаем арифметически, чтобы найти ответ (U).
Вот этому и надо учить ученика. Тогда решение задач станет обучением, а не в просто демонстрацией.
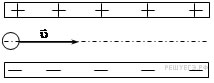 Задание из ЕГЭ (11 кл.) Пылинка, имеющая массу 10-8 г и заряд – 1,8·10-14 Кл, влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между егопластинами (см. рисунок, вид сверху) Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме. Задание из ЕГЭ (11 кл.) Пылинка, имеющая массу 10-8 г и заряд – 1,8·10-14 Кл, влетает в электрическое поле вертикального высокого конденсатора в точке, находящейся посередине между егопластинами (см. рисунок, вид сверху) Чему должна быть равна минимальная скорость, с которой пылинка влетает в конденсатор, чтобы она смогла пролететь его насквозь? Длина пластин конденсатора 10 см, расстояние между пластинами 1 см, напряжение на пластинах конденсатора 5 000 В. Система находится в вакууме.
Решение от составителей задачи.

Не находите, что на детей это решение скорее всего произведет обескураживающее действие! Как решение задачи оно идеально (что, к сожалению, не всегда характерно для заданий ГИА и ЕГЭ). Догадайтесь, какие вопросы могут возникнуть у учеников, и на которые здесь нет прямого и ясного ответа.
Подскажем. Как начинают решение таких задач (а не только этой)? С какой стати «сила, действующая на частицу»? Откуда можно узнать, что потребуется в начале задачи «связь напряженности с напряжением» и тут же (совсем из другой части физики) второй закон Ньютона? Откуда всё это берется? Почему? Как до всего этого догадаться??? И как решение этой задачи может подсказать пути решения других задач по этой теме. Например, такой:
Задание из ЕГЭ (11 кл.) На непроводящей горизонтальной поверхности лежит проводящая жесткая рамка из однородной тонкой проволоки, согнутой в форме квадрата АСDЕ со стороной, равной а. Рамка, по которой течет ток I, находится в магнитном поле, вектор индукции В которого направлен перпендикулярно сторонам АЕ и СD. При каком значении модуля вектора магнитной индукции поля рамка начнет поворачиваться вокруг стороны СD, если масса рамки m?
Что общего в решении этой и предыдущей задачи? А если эта связь не столь очевидна, тогда чему может научить разбор предыдущей задачи? – Решать только одну эту задачу? Столько усилий и так мал результат?
Приведем далее пример решения еще одной задачи из ЕГЭ.
Задание из ЕГЭ (11 кл.) Маленький шарик с зарядом q = 4·10-7 Кл и массой 3 г, подвешенный на невесомой нити с коэффициентом упругости 100 Н/м, находится между вертикальными пластинами плоского воздушного конденсатора. Расстояние между обкладками конденсатора 5 см. Каково напряжение между обкладками конденсатора, если удлинение нити 0,5 мм?
Запишем краткое условие:
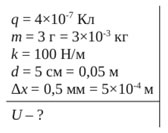 Если надо найти напряжение, то логично с него и начать решение задачи, а не с того, что нравится какому-то дяде. Напряжение между пластинами конденсатора: Если надо найти напряжение, то логично с него и начать решение задачи, а не с того, что нравится какому-то дяде. Напряжение между пластинами конденсатора:
U = Ed.
Не слишком впечатляет, успокаивает лишь то, что d дано, впрочем, остается только узнать Е и задача будет решена.
Из известных нам формул напряженности, есть подозрение, что
E = Fэл/q
самая подходящая, ибо q известно. Значит искать надо силу Fэл.
 Теперь понятен план решения задачи: Теперь понятен план решения задачи:
- найти Fэл (по второму закону Ньютона);
- найти напряженность Е;
- найти напряжение U.
Решение задачи:
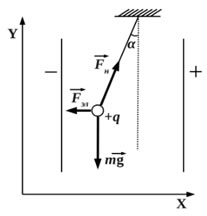
Чтобы воспользоваться вторым законом Ньютона, сделаем чертеж сил, действующих на шарик. Мы можем обнаружить три силы: Fэл, Fн, mg и можем составить уравнение сил (II закон Ньютона):
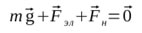
В проекциях на оси координат:
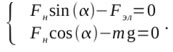
Или иначе: 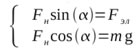
Анализируем на предмет полезности (решаемости) полученной системы уравнений. Три неизвестных (Fэл, Fн, α) многовато для двух уравнений…
Проблема: избавиться от хотя бы одного количества неизвестного. Это не трудно, ибо Fн = kx и Fэл = Eq.
Применим также нестандартный приём для избавления от ненужного ни для чего α, возведем оба уравнения в квадрат и сложим верхнее уравнение с нижним:
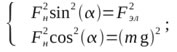
или, используя основное тригонометрическое тождество:
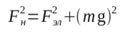
Подставляем сюда формулы сил Fэл и Fн: 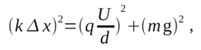
выразим отсюда искомое U:
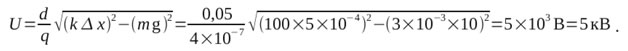
Можно избежать возведения в квадрат уравнений системы. Просто из нижнего уравнения системы выразить cos(α) = mg/Fн, по косинусу найти синус (опять же через основное тригонометрическое уравнение), а по синусу найти Fэл.
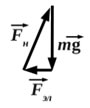 А можно и совсем сократить решение задачи. Если внимательно посмотреть на векторное уравнение II закона Ньютона и чертёж сил справа от него, то можно увидеть следующую интерпретацию этого уравнения через геометрию (см. рис.справа): А можно и совсем сократить решение задачи. Если внимательно посмотреть на векторное уравнение II закона Ньютона и чертёж сил справа от него, то можно увидеть следующую интерпретацию этого уравнения через геометрию (см. рис.справа):
По теореме Пифагора сразу получаем: 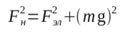
Во всяком случае, если решение ученика отличается от нашего, мы никогда не снижаем за это оценки, даже если оно на наш взгляд не самое рациональное.
Чем это будет полезно для решения двух выше приведенных задач из ЕГЭ?
Попробуйте ответить сами. В первой начните с рассуждений о скорости (ведь ее надо найти), а во второй – с формул магнитной индукции (формулу Амперовой силы), и вполне логичным (но не обязательно простым) образом перед вами раскроется решение и этих задач. Каждая новая задача показывает своеобразие применения нашего алгоритма к тому или иному типу задач, сам же алгоритм не меняется.
Сложные задачи мы также заставляем заучивать с решениями и рассуждениями. Образцы, если они добросовестно заучены, живут в человеке своей собственной жизнью. Они способны образовывать «кусты ассоциаций» (П.М.Эрдниев), собирая материал в единую структуру знаний в противовес «клиповому (обрывочному) мышлению», столь характерному для современного человека.
Обратите также внимание, что наше (может быть для кого-то неуёмное) желание всё разжевать и объяснить делает решение задач ЕГЭ части «С» достаточно простым и доступным, в том числе и для очень среднего ученика. Наши средние ученики на ЕГЭ набирают 60-70 баллов, а слабые 40-50. Но главное их достижение даже не в поступлении в тот или иной вуз, а в том, что они успешны там в изучении физики.
Если вы дочитали статью до конца - вы гений!
И можете кликнуть внизу кнопку "Оценить!" Заранее спасибо!
© 2016. Смирнов Н.В., учитель физики, Санкт-Петербург.
Библиография
1. Балл, Г.А. О психологическом содержании понятия «задача» / Г.А. Балл // Вопросы психологии.– 1970.– № 5.– С. 81-87.
2. Зайцева, С.А. Организация работы над текстовой задачей на основе модели. / С.А. Зайцева, И.И. Целищева // Начальное образование.– 2007.– № 4.– C. 9-15
3. Кулагина, И.Ю. Возрастная психология: Учебное пособие / И.Ю. Кулагина.– 3-е изд.– М.: УРАО, 1997.–176 с.
4. Фридман, Л.М. Как научиться решать задачи: Кн. для учащихся ст. кл. средн. шк. / Л.М. Фридман, Е.Н. Турецкий.– 3-е изд., дораб.– М.: Просвещение, 1989.– 192 с.: ил.
5. Целищева, И. Как помочь каждому ученику самост-но решать текстовые задачи / И. Целищева, С. Зайцева // Нач. шк.: еженед. прил. к газ. "Первое сентября".– 2001.– 00.05 (№ 18). – С. 2-5.
6. Шикова, Р.Н. Использование моделирования в процессе обучения решению текстовых задач. / Р.Н. Шикова // Начальная школа: ежемес. науч.-метод. журн.– 2004.– № 12.– С. 32-41.
7. Лукашик В.И. Сборник задач по физике. 7-9 классы: пособие для учащихся общеобразоват. учреждений/ В.И.Лукашик, Е.В.Иванова. – 24-е изд. – М.: Просвешение, 2010. 240 с.: илл.
 |