В статье описан метод обучения решению задач по физике с опорой на использование пособия-справочника формул; метод, который одинаково применим при обучении и сильного, и слабого ученика и, в известной мере, уравнивает их возможности в обучении.

При  решении задач мы исподволь пользуемся воспоминаниями, а нам кажется, что мы  решаем задачу. И объясняя, как надо решать задачи, мы бессознательно  используем  механизмы воспоминания вместо  механизмов решения, а потому учим плохо (не учим решать). Ведь наш ученик не  помнит того, что помним мы - учителя - о решении задач. А мы еще позволяем себе  его упрекать в этом! Как же учить решать того, кто мало знает о решении задач? Прежде всего, сами научимся решать  задачи, а не вспоминать готовые решения.
      Приглядимся  к тому, как нормальный человек решает ту или иную проблему (задачу).  Это наблюдение обещает быть полезным, ибо  только этому и надо будет учить нашего ученика, когда он придет к нам на урок.

А  теперь конкретно.
        Покажем,  как нашим способом можно решить одну из несложных задач части С (С3) из  материалов ЕГЭ. Затем покажем, как эту же задачу обычно решают в школе.  Любопытно сравнить.

В горизонтальном  цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный  идеальный газ. Давление окружающего воздуха p = 10⁵ Па. Трение между  поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения  от газа отведено количество теплоты Q = 75 Дж. При этом поршень передвинулся на  расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?

Не  будем даже записывать кратко условие задачи, так как наш ученик не всегда  знает, как что называется и какой буквой обозначается (но мы обучаем решению  задач и таких учеников тоже).
          Первое. Выделим ключевые слова, те, которые, как  кажется ученику, обозначают физические величины или понятия: «идеальный газ»,  «количество теплоты».
Поищем,  где встречаются эти слова. Мы, знающие, ищем в голове, а незнающие полезут в  справочник: Q  = cmΔt; Q = λm; Q = rm; Q = qm; Q  = ΔU  + A’; Q = I²Rt.
Наступает  время выбора из множества. Вместе  ключевые слова сходятся в формуле первого закона термодинамики: Q  = ΔU  +  A’.
Хорошо  бы, были такие справочники, в которых все выстроено не по темам (долгонько  искать незнающему-то), а по алфавиту, и все искомое на одной странице, и сразу  можно понять, что и как обозначено в формуле. Но, допустим, у нас именно такой  справочник.
Что-то  нашли, но ответ пока не виден. До неизвестной площади S пока - ой как! -  далеко, но мы ребята упертые! А, главное, верим в силу алгоритма.
Второй шаг. Поищем в том же  замечательном справочнике, как можно выразить  ΔU  и A’ через одни и те же величины, ведь Q нам известно:
а)  Внимание! Для выбора формулы работы газа A’ всегда надо знать процесс,  происходящий с газом. В данной задаче это проблема. Если внимательно прочитать  условие, можно понять, что поршень никто намеренно не удерживает, трение мало.  Это значит, что давление внутри цилиндра и снаружи одинаково и не меняется (!)  – мы имеем процесс с постоянным давлением, для которого
A’ = pΔV  = - pxS (объем уменьшается).
Это  соотношение очень полезно, так как позволит нам в дальнейшем связать между  собой величины из условия задачи: x, S и Q (вот и забрезжил свет в конце  тоннеля).
б)  Тут же в справочнике:  ΔU = 3/2 νRΔT = 3/2 pΔV =  - 3/2pxS.
Третий шаг. Теперь осталось  собрать в одну формулу найденные нами зависимости: Q  = ΔU  + A’ = - 3/2pxS – pxS = - 5/2  pxS.
Подставив  сюда значение данных нам величин, легко найдем ответ: S = - 2Q/(5px) = 30·10^-4 м² = 30 см².
Заметим,  что Q = - 75 Дж, так как «от газа  отведено количество тепла».
Ответ: S = 30 см².

Теперь  решение, как его дают обычно в школе.

Воспользуемся  первым законом термодинамики: Q  = ΔU  +  A’.(А почему???)
        Подставим  сюда формулы изменения внутренней энергии и работы газа: ΔU = 3/2 νRΔT = 3/2 pΔV =  -  3/2pxS.    A’ = pΔV  = - pxS. (Ловко! А откуда вы все это взяли???)
        Тогда  получим: Q  = ΔU  + A’ = - 3/2 pxS – pxS = - 5/2 pxS.
        Откуда: S = - 2Q/(5px) = 30·10^-4 м² = 30 см².

Сравним  для ясности. Сколь много вопросов без ответов возникает у ученика в таком  решении. Насколько необоснованными (для мало знающего ученика, конечно)  выглядят действия учителя! Сколь много подразумевается того, что должно было  быть высказано. Как много возложено на плечи учеников того, что мог бы и должен  был взять на себя учитель! А как использовать это решение? Запомнить как  решение одной из задач? Так мало? Так беспомощно?

Обратите  внимание. Алгоритм, предложенный нами, годится для решения любой школьной  задачи и не только по физике. В нем четко распределены роли: что делается в  слепую по алгоритму, что берем в качестве знания (из головы или справочника),  где все дело за нами (принятие решения, выбор). Вот, только где бы взять такой  удобный для ученика справочник формул?
        И  главное. Мы, пытаясь решить задачу, прошли по лабиринту, ранее не хоженому  нами. За каждым поворотом нас ожидало новое интеллектуальное приключение, новый  поворот, новый вопрос и поиск ответа. Как все это далеко от второго решения.  Да, решение в обоих случаях по сути одно и то же. И все же, все же.

Работая  по такому алгоритму, часто наши изначально не слишком умелые дети находят не  одно, а два и более решения. Не мудрено, ведь они обращаются сразу ко всему  массиву возможных формул (зависимостей, законов). А запомнить (заучить) им  нужно только один алгоритм (и небольшое количество приемов), а не решение  полутора тысяч задач из школьного задачника. А их готовность к решению вовсе  неизвестных задач! И не имеет значения, относится ли задача к одной теме  (например, сугубо колебательный контур) или включает в себя еще и механику, и  термодинамику и т.д. (ведь в поиске по алфавиту мы в справочнике получаем  доступ сразу ко всему массиву формул данной величины).

Толково  ли я объяснил здесь разницу? Понятен ли вам выигрыш и его истоки?
        Приведем  примеры решения других задач. Например, С5.

В идеальном  колебательном контуре, состоящем из конденсатора и катушки индуктивности,  амплитуда силы тока I_m = 50 мА. В таблице приведены значения  разности потенциалов на обкладках конденсатора, измеренные с точностью до 0,1 В  в последовательные моменты времени. Найдите значение электроемкости  конденсатора.

1.  Ключевые слова условия задачи -  «колебательный контур», «емкость» - дают  по справочнику: C = q/U;  C = ε ε₀S/d; W = CU²/2;.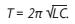
        Выберем  формулу Томсона (есть подозрение, что Т мы найдем по таблице):
        
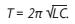
         или, возведя в квадрат, T² = 4π²LC.

2.  Осложнение: неизвестные индуктивность L и  период Т. Среди прочих формул L обратим внимание на энергию магнитного  поля: W = LI²/2
        Вместе  с формулой энергии конденсатора W = CU²/2 (которая уже раз мелькнула перед нами) можно составить уравнение сохранения  энергии при колебаниях (максимальная энергия магнитного поля катушки равна  максимальной энергии конденсатора):
        LI_m²/2  = CU_m²/2. Это часто встречающийся прием, на который раз за разом надо обращать  внимание. Таких приемов немного в решении задач.
        Здесь  I_m  нам дано по условию  задачи, а U_m можно найти в таблице (наибольшее значение напряжения).
        Отсюда: LI_m² = CU_m²;        L = CU_m²/ I_m².

3.  Подставим значение индуктивности в формулу Томсона:
        T² = 4π²C· CU_m²/ I_m².
        Извлечем  квадратный корень из обеих частей уравнения и выразим С:
        C = Т I_m /  2πU_m.

4.  Период колебаний найдем в таблице как время полного цикла колебаний (Т = 8 мкс). Поскольку все величины  известны, подставляем численные значения и получаем ответ.
        Ответ:  С ≈ 16·10^-9 Ф = 16 нФ.

В  этом решении четче видно то, что мы называем   «интеллектуальным путешествием с препятствиями по лабиринту формул»  (число которых для ученика представляется бесконечным). Отыскали формулу  Томсона, да не тут-то было. Нашли формулу, связывающую ток (дано по условию  задачи) и индуктивность (промежуточное неизвестное). Далее потребовалось умение  использовать закон сохранения энергии (ну, наш ученик ходит на уроки, где-то  слышал о сохранении энергии, имеет какие-то представления о колебательных  процессах, чтобы по таблице найти максимум напряжения и период колебаний).

Опора  на ключевые слова, умение выделять главное – одно из важнейших надпредметных  умений, необходимых человеку в информационном мире, которое мы усиленно  развиваем у нашего ученика.

Все  справочник, справочник... А как же знания самого ученика? На первое место мы  ставим успех (сиречь – вера!), а знания появятся как неизбежная объективная  необходимость по мере накопления опыта (становится более понятным, для чего  зубрить).  И еще, становится понятной  особая важность точного знания, не  приблизительного, каким грешат у нас многие.

Задача A19.

В области пространства,  где находится частица с массой 1 мг и зарядом 2 нКл, создано однородное  горизонтальное электрическое поле напряжённостью 50 В/м. За какое время частица  переместится на расстояние 0,45 м по горизонтали, если её начальная скорость  равна нулю? Действием силы тяжести пренебречь.

Ответы:   1) 95 с        2)  4,2 с        3) З с        4) 9,5 с.

1.  Ключевые слова: масса, заряд, напряженность, время и расстояние.
Время и расстояние: s = vt; s = (v + v₀)t/2;  s = v₀t + at²/2; N = A/t; FΔt = Δp. Упоминание  в условии задачи начальной скорости приводит нас к выбору: s = v₀t + at²/2 = at²/2.

2.  Осложнение: мы не знаем ускорения a,  без которого ничего не решить.
Из  кучи формул ускорения выберем ту, которая не содержит времени (нам его потом  надо будет найти):  F = ma.

3.  Массу m мы знаем по условию  задачи, это вдохновляет, но теперь новая проблема – сила F.

4.  Из всех сил выбираем по смыслу электрическую: F = kq₁q₂/r²; F = Eq. Последнее  предпочтительнее, так как в условии упоминаются напряженность и заряд.

5.  Собираем найденное вместе: ma = Eq; a = Eq/m.  Далее: t² = 2s/a = 2sm/(Eq).

Задача  решена: t = 3 с. Правильный ответ №3.

Пять  неочевидных для ученика шагов в задаче! Пять крутых поворотов, за которыми не  виден результат. Как в романе! Целое детективное расследование. А многие ли  ученики рискнут взяться за решение задачи, когда они не видят всего пути  целиком, от начала и до конца. И как мало в этой задаче, в отличие от  предыдущей, надо понимать в физике (что упрощает жизнь тем, кто у нас пока  неуспешен). Полностью выручает работа со справочником (формальное знание).  Алгоритм плюс знание. Плюс математика.

Задача  С5.

В идеальном  колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5  мА, а амплитуда колебаний заряда конденсатора 2,5 нКл. В момент времени t сила  тока в катушке равна 3 мА. Найдите заряд конденсатора в этот момент.

1.  Ключевые слова: колебательный контур, сила тока, заряд, конденсатор.
        По  справочнику имеем в распоряжении формулы: 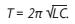, ω = 2π/T; q =q_mcos ωt; i =i_m sin ωt; W_эл = CU²/2;  W_м =  LI²/2.

ФИПИ рекомендует начинать решение задачи с закона сохранения  энергии, но есть и другое решение.  Для наших детей очевиднее выбрать уравнения заряда и тока (этих величин много в  условии задачи): q =q_mcos ωt; i =i_m sin ωt.

Знание амплитуды тока и текущего значения тока позволят нам  найти sin ωt (пока не понятно зачем, но для наших детей «можно», значит  надо попробовать).
        Итак, 3 = 5 sin ωt; значит sin ωt = 3/5.

2. Как бы это использовать? Синус позволит найти косинус,  который мы видим в формуле колебаний заряда. Основное тригонометрическое  тождество: 1 = sin² ωt + cos² ωt. Откуда cos ωt = ± 4/5.

3. Зная текущее значение cos ωt, найдем текущее значение заряда, ведь максимальный заряд нам  известен: q = q_mcos ωt = ± 2,5·4/5 = ± 2 (нКл). В отличие от ФИПИ мы нашли иное  решение и два правильных ответа вместо одного.

Итак, написать решение - не значит решить задачу. Решить –  это совершить ряд последовательных действий, в каждом из которых необходимо  сделать выбор, что, между прочим, далеко необязательно сразу приводит к ответу,  а, скорее всего,  приведет к новым  вопросам и потребует новых шагов. Решать - значит двигаться в определенном  направлении в условиях неочевидности.
        Наши дети довольно часто оказываются в тупике. Ой, как это  полезно. Мы не ставим за это плохую оценку. Попытка, пусть неудачная, тоже  требует своей работы над задачей. Отрицательный результат бывает более полезен,  чем положительный. А многие, пройдя через несколько неудач, понимают, что  где-то надо было пойти другим путем.
        Наш подход делает обучаемыми гораздо большее количество  детей, чем это обычно бывает. Наш ученик оптимистичен. Он знает, всегда есть  варианты.