То, что российское образование сильно упало за последнее время и продолжает свое падение, является уже общим местом. Как с этим быть, и что делать?
Министерство образования и науки РФ дает учителям пример того, как следует действовать для повышения уровня образования школьников. Оказывается достаточно понизить минимальные баллы ЕГЭ и количество не усвоивших программу школы по русскому языку и математике сразу уменьшится, а уровень образования вроде как возрастает! Справедливости ради надо сказать, что Министерство здравоохранения одной из областей России все-таки превзошло всех! Они выдали план скорой помощи - не более 1 покойника в неделю! Это сильно! Какая характерная степень отсутствия какого бы то ни было понимания чиновником реальности! А что делать в этой ситуации самой скорой помощи? Лишних на помойку выбрасывать? Или записывать во временно живых, как это сделало с неуспевающими Минобрнауки?
Не хороший пример, постыдный и недальновидный. Больно от всего этого!
Что в силах учителя? Стараться лучше учить своих учеников, по возможности не обращая внимание на грохочущие вокруг грозы. Делать свою работу по сути, а не для отчетности.
В чем сказываются особенно недостатки теперешнего образования? Нынешние дети и знать могут многое, и с источниками информации могут работать, когда им это надо. Но в из знаниях нет системы, нет глубины. Их знания поверхностны и обрывочны, иначе говоря, калейдоскопичны. Их мышление можно назвать «клиповым» мышлением, мышление в котором легко путаются местами причина и следствие, нарушены логические связи, исторические последовательности (см. например
http://emosurf.com/post/3709). Но страшнее, что им от этого не стыдно и не больно. Ну, перепутал… Их мышление безответственно. Может быть они смогут занимать в будущем высокие посты, но из них не смогут вырасти государственно ответственные мужи.
Зачем учителю думать об этом? Есть методисты, они пишут методички, мы их исполняем. Есть НМЦ и РМЦ, есть система повышения квалификации, там скажут, как надо делать.
А вот хочется быть хорошим учителем, хорошо учить детишек! Чтобы не дежурными словами дети прощались с нами на выпускном. Но еще важнее, чтобы им было легче потом жить, чтобы умели думать и отвечать за свой выбор! И многое ли сможет взять от методистов тот учитель, который нацелен только исполнять, кто не смеет иметь своей системы взглядов на обучение и воспитание, пусть даже для начала наивной, простой?
Как всему этому может помочь преподавание физических теорий в школе? Думается, в известной мере, да!
Обычное, пусть даже добросовестное изложение материала параграфа нам кажется недостаточным. Для нас важно использовать объяснение темы для обучения различным способам научного мышления (в противовес бытовому), научного способа решения проблем, способствовать развитию их мышления, но на конкретном примере. Думается, только такой подход истинно обучает тому, как надо размышлять.
Часто приходится видеть, листая конспекты уроков учителей, что учитель ставит целью развивать мышление учеников. Так и хочется спросить: «А какое именно интеллектуальное качество (свойство, умение) ученика ты хочешь развить на данном уроке, в данном упражнении?» Или так, вообще… Для красного словца?
Другой путь – специальные упражнения для развития интеллекта, пусть на физическом материале, но не связанные напрямую с уроками физики, скорее заменяющие уроки физики отдельно от предмета висящие в интеллектуальном пространстве ребенка. Тут не понятно, какой результат может дать выполнение таких упражнений, как упражнения на сравнение, анализ, синтез, дедукцию и индукцию, систематизацию и классификацию и пр. (См., например, «Развитие интеллекта учащихся при обучении физике», Курко О.А., учитель физики). Большинство детей могут мыслить преимущественно конкретно, а переносить материал из одной области знаний в другую для многих и многих весьма затруднительно.
Еще пример в статье «Развитие интеллектуальных и практических умений обучающихся на уроках физики» Рудометовой Н. И., где указана цель: сформировать знания о мыслительных операциях и процессах, связанных с мышлением.
Все эти нагромождения по нашему мнению ничего не дают ученику для его развития, отвлекая от главного. Ну, и что, что наш ученик будет знать, что соединение высказываний в более сложное называется конъюнкцией? Разве он станет от этого лучше соображать? Нет, конечно! Это мы должны четко знать, чем отличается логически более жесткая конъюнкция от более свободной дизъюнкции. И суметь это объяснить доступно ученику, не перегружая его избыточной терминологией.
В нашем понимании изучение теории физики это и есть способ развития интеллекта школьника. Ничего не нужно выдумывать сверх того, если мы не только излагаем материал параграфа, но и учим рассуждать, как рассуждали великие, беря их труды за образец. Нет необходимости в специальных упражнениях или специальных знаниях для развития интеллекта. Сама физическая наука учит мыслить, ибо любая теория (или ее фрагмент) может быть прекрасным примером, образцом решения научной задачи, неизменно включающая в себя все своеобразие, что особенно важно, подходов физической науки (ибо у каждой науки свои средства и цели).
Чтобы мы смогли действительно обучить учащихся умению рассуждать в стиле физической науки, чтобы наши слова не пропали с последним нашим словом на уроке, мы не только обращаем внимание во время изложения темы на способ решения теоретического вопроса в физике, но и требуем заучивания образца рассуждений, осмысления его и обязательного воспроизведения. А перед каждым таким уроком выделяем для себя, какие мыслительные операции потребуется проделать, чтобы изложить материал, и на этих операциях и сосредотачиваем внимание учеников на самом уроке.
Чтобы было понятно, приведем примеры уроков.
Пример I. Первая серьезная встреча учеников с теорией в седьмом классе происходит на уроке «Действие жидкости и газа на погруженное в них тело. Вывод формулы архимедовой силы».
Опуская само собой понятные вещи, сосредоточимся на главном для нас. Во-первых, здесь используется
дедуктивный подход, как во всяком законе. Из общего (формулы архимедовой силы) получают частные результаты: решения конкретных качественных и количественных задач, практических заданий и пр. Между тем известно, что движение мысли от общего к частному, дается ученикам в силу возрастных особенностей много труднее, чем от частного к общему. Далее, вывод формулы построен
на алгебраических преобразованиях. Формулы сил F
1 (сила давления сверху) и F
2 (сила давления снизу) заменяем их выражением через давление: F = pS. Давление жидкости p заменяем формулой p = ρ
жgh, V = hS и т.д. Для ученика не очень простой будет такая длинная цепочка последовательных преобразований. И к этому он уже должен быть готов на примере решения всех и всяческих задач в предыдущих темах, иначе крах!
Кроме того, большое значение здесь будут иметь
индексы. Иначе трудно будет понять почему вес, но жидкости, а не тела. Почему объем не всей жидкости, а только ее части в объеме тела (вытесненной телом)?
Теперь планируем урок.
1. Опыт, показывающий факт уменьшения веса тела, погружаемого в жидкость (явление выталкивания). Постановка проблемы. Любой физик задастся вопросами:
а)
Почему тело весит меньше, будучи погруженным в жидкость? Требуется объяснение наблюдаемого.
б)
На сколько меньше весит,
от чего это зависит? (Замеряем вес бруска на воздухе и в жидкости, находим разницу весов. Используем это число в конце урока, а пока фиксируем его на доске.)
В этих вопросах заключено гораздо большее, чем может показаться. В них дух физики. В них заключено то, что в первую очередь думает физик, сталкиваясь с новым явлением. Поэтому эти два вопроса фиксируем на доске (экране) до окончания урока. Это важно! Противопоставляйте из урока в урок научные подходы бытовым суждениям.
Лирическое отступление. Бытовизмы наш страшный враг. Если мы хотим мыслить научно, то и надо быть последовательным, говорить о физике не бытово. Если мы проводим сравнение, то научное сравнение предполагает поиски и сходства, и различия, а не только одного из них. Если мы идем в рассуждениях индуктивным путем, или путем аналогии, будьте любезны проверить опытом полученный результат, и т.д. Это рождает культуру мышления. Правда, это усложняет жизнь, заставляет делать дополнительную работу. Но только тогда строгость в нашем научном мышлении перейдет в наших учеников и породит ответственность высказываний.
Научное мышление, как наиболее точное и строгое, а не надуманное учеными, чтобы «дурить» народ. Приверженность к научному способу мышления должна давать позитивный результат и в быту. Научное не в противовес бытовому, а как идеал для развития повседневного мышления. Чтобы это стало так, учителю на уроке надо мыслить предельно убедительно, «чисто», максимально доказательно, абсолютно строго. Бытовое мышление не обязательно предполагает мужество мышления, как мужество возможного отказа от своих взглядов, если вскроется их ошибочность, или мужество свергать авторитеты не ради того, чтобы засветиться, а только, когда за тобой сила истины. Бытовое совсем не обязательно по правде, а не по лжи. Часто бытовое мышление реагирует на ложь лишь, когда это выгодно субъекту мышления. Нравственная составляющая, критичность, ответственность на бытовом уровне могут быть занижены.
Какими путями научное мышление (да просто правильное) может стать привычным для нашего воспитанника? Самое сильное средство здесь, пожалуй, дискуссия. Дискуссия, как допущение иного мнения, как разговор на равных. На первое место здесь выходит владение предметом и умение вести дискуссию. И здесь абсолютно недопустимо ощутить хоть раз свою уязвленность. (См. пример в Приложении 1).
Другой наш враг на пути развития ученика – псевдонаука. Мы должны не запретить ее, а научить четко опознавать ее среди многочисленных гуляющих в народе веяний. Узнавать по строгим критериям. Их дать тоже наша задача.
Наша основная цель в преподавании физики перебороть бытовое мышление, посеять веру в силу научного подхода к изучению природы, добиться, чтобы и дома ученик мыслил в нашем ключе.
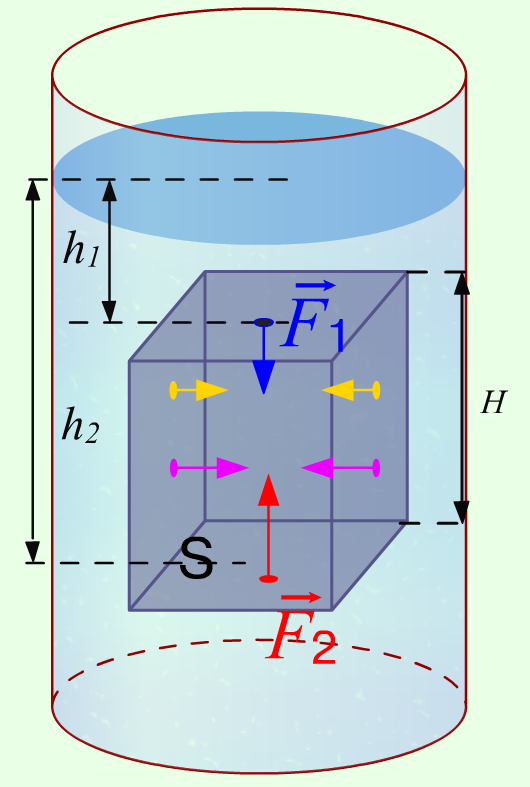
2. Последовательно пытаемся найти ответы на два наших вопроса.
а) Из предыдущих уроков напоминаем, что тело погруженное в жидкость испытывает давление с ее стороны. Оно зависит от глубины погружения: p = ρ
жgh. Но нижняя грань бруска погружена глубже, чем верхняя. Вот и причина уменьшения веса: снизу жидкость давит сильнее, чем сверху. Делаем рисунок. Кратко записываем объяснение появления эффекта выталкивания тела. Даже можем уже записать: P
ж = P - F
выт; (вес в жидкости меньше веса на воздухе на величину выталкивающей силы) и F
выт = F
2 – F
1 (выталкивающая сила объясняется разным давлением на нижнюю и верхнюю грани тела).
б) Второй вопрос. Мы уже начали искать ответ на него. Важно: из правильного объяснения явления в физике всегда следует правильное количественное выражение закона.
Упростим себе задачу. Это наше действие тоже четко позиционируем, как прием, часто используемый физиками. Выберем тело правильной формы (параллелепипед с гранями параллельными поверхности жидкости). Однако вслед за упрощением, всегда должен следовать возврат к усложнению (а если тело неправильной формы), к которому обратимся в конце урока, но без которого наши рассуждения нельзя считать полными (строгими). В учебнике эта строгость опущена, как если бы это было в науке допустимо (?)
Поработаем с формулой F
выт = F
2 – F
1. Вместо F
2 и F
1 подставим F = pS с соответствующими индексами, а давление заменим на p = ρ
жgh. И далее следуем обычным путем по учебнику. Что для нас важно, что этот вывод не очень прост для ученика, поэтому сложное делим на части.
Каждую процедуру пишем
в отдельной строке, позиционируя как отдельное действие, вовсе не как в учебнике, все в одну строчку. Для многих учеников визуально это выглядит несваримой кашей.
Добираемся до первого итога: F
выт = ρ
жgV. Это промежуточный, но очень важный для решения задач результат. Выделяем его в рамочке в наших записях.
Что значит эта формула? В ней ρ
жV = m, но чья это масса. Показываем, как по индексам установить, что это масса вытесненной телом жидкости, mg = P. Раз масса вытесненной жидкости, то и вес той же самой жидкости. Формулируем закон Архимеда: на тело, погруженное в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной жидкости (или газа). Поясняем ровно как в учебнике, причем здесь газы.
По ходу вывода формул мы делали ряд допущений. Мы решили, что причина потери веса при погружении тел в жидкость или газ является разная глубина погружения верхней и нижней частей тела, выбрали для простоты тело правильной формы. В этом есть элемент нестрогости, поэтому обязательно
требуется проверить наши выводы, на телах правильной и неправильной формы.
3. Критерием истины в физике является
опыт. Какой это опыт нам подтвердит правильность выводов? См. формулировку закона Архимеда! Измерим объем нашего тела, измерим с помощью водоотливного сосуда, сколько воды вытеснило тело. Сравним вес вытесненной воды и величину архимедовой силы по формуле F
выт = ρ
жgV. В пределах допустимой погрешности видим равенство веса вытесненной воды, архимедовой силы и измеренной нами ранее потери веса. Вот на сколько тело становится легче! Закон выведен правильно!
Домашнее задание.
1. Мы взяли тело правильной формы. А если тело будет неправильной формы? Доказать, что закон будет правилен и для такой ситуации. Это очень сложный вопрос для семиклассников. Тут требуется дифференциальный подход, позволяющий применить ранее сделанный вывод и к телу неправильной формы, разбивая его на большое число маленьких правильных кубиков, а затем складывая результат (интегрируя), чтобы получить силу, действующую на все тело целиком. Это смогут сделать лишь очень сильные ученики, а может и никто не справится. Не беда. Мы покажем этот важный прием на следующем уроке тем более, что он еще не раз встретится в старших классах.
2. Выучить вывод закона со всеми словами и оговорками (от цифры 1 до цифры 3 включительно). Параграфы из учебника в помощь.
Что спросим на следующем уроке? Еще раз в быстром темпе повторим вывод, а затем кто письменно, кто устно на флэшку или комп с микрофоном.
Как там наш троечник, о котором мы так пеклись в предыдущей статье о решении задач? Выучить у всех получится? Думаю, что нет. А мы скажем в комментарии к домашнему заданию, выучи то, что тебе по силам, но честно. Трудно с алгеброй? Ладно, пропустим, но делай, что можешь честно, выучи хотя бы все опыты, 3 итоговые формулы и формулировку закона Архимеда наизусть!
Чему мы в итоге научили ученика?
1. Мы показали ученику,
как рассуждает физик при решении научных задач, какими вопросами он задается. Если мы в дальнейшем будем последовательны, то нам удастся сформировать представление об особенностях работы и способах мышления физиков.
2. Мы показали, что имея некоторые законы (формулы), и, исходя из некоторых представлений о протекающем явлении,
с помощью алгебраических преобразований мы можем получать новые законы, описывающие это самое явление.
3. Мы показали прием, часто используемый физиками, -
упрощение. Мы также показали, что упрощение всегда требует возврата к более сложному случаю для полноты рассмотрения предмета, и либо распространения выводов в область более сложного случая (экстраполяция), либо установления границ применимости результатов. Кроме этого все выводы в физике
проверяются на опыте. Мы показали, что уважение к строгости и доказательности в физике не уступает этим качествам в математике.
4. Мы показали, что во многих случаях при решении теоретических задач не лишним будет уделять внимание всяким мелочам, таким, например, как
индексы.
5.
Дедуктивное мышление в нашем случае проявит себя при решении задач различного толка. Законы физики в материальном мире играют роль бога. Они абсолютно непреложны, что вовсе не однозначно в восприятии учеников. Непреложны значит, что при решении задач любого толка мы обязаны начинать с закона, а не выдумывать по ходу «новые», удобные для быстрого решения данной задачи, как часто стремятся делать наши ученики. Многие из них пытаются подтасовать закон под решение задачи вместо того, чтобы от закона дедуктивным путем идти к решению, пусть даже и не совсем очевидным способом. Такие привычки к «изобретению» всё новых закономерностей проистекают от губительных на наш взгляд для обучения физике «задач на сообразительность». Они создают иллюзию развития мышления, а на самом деле способствуют преувеличенному развитию интуитивистского подхода к решению задач на уровне «здравого смысла», не уходящего слишком далеко от заурядного бытовизма, несмотря на всю привлекательность, ибо эти задачи часто основаны на неожиданных парадоксах. Нынешняя физика такова, что предугадать интуитивно характер физических законов, лежащих далеко за пределами бытовых представлений о мире, оказывается просто не возможным.
Пример II. Первый закон Ньютона.
Не будем приводить здесь строки из учебников по выводу первого закона Ньютона. Остановимся лишь на следующем.
Самые глубокие законы физики могут быть выведены только индуктивным путем, от частных примеров к обобщению результатов. Так мы выводим и закон сохранения энергии, в разных разделах физики натыкаясь на факт неизменности энергии в тех или иных обстоятельствах. Так мы получаем и Первый закон Ньютона.
Надо иметь ввиду, что движение по индуктивной логике никогда ничего не доказывает, а лишь указывает нам на характер возможного закона (закономерности). Поэтому, строго говоря, утверждения полученные индуктивным путем, следует проверять на практике. Это наш ученик должен четко понимать, если мы хотим говорить о следовании принципу научности.
Большой торт не едим целиком, а всегда делим на кусочки по размеру ртов. Не один, а несколько опытов и мысленных экспериментов не просто запомнить, особенно учитывая, что из них мы должны сделать определенные выводы. Поэтому выручит ученика здесь конспект лучше в шаталовской форме, или хотя бы так, как показано ниже.
1. Опыт с шариком. Земля – шнур: уравновешивают друг друга (компенсируют). Состояние: покой.
2. Мысленный эксперимент Галилея. Земля – желоб: уравновешивают друг друга. Состояние: равномерное движение сколь угодно долго.
3. Справедливо не во всех системах отсчета. Инерциальные системы отсчета.
4. Формулировка I закона Ньютона.
Формулировка первого закона достаточно трудно запоминается учениками, поэтому ее мы тоже делим на части и записываем в тетрадь смысловыми отрезками:
Существуют такие системы отсчета (инерциальные), относительно которых
поступательно движущиеся тела сохраняют свою скорость постоянной
(движутся по инерции), если
на них не действуют другие тела,
или действие других тел компенсируется.
Каждую строчку этой записи (форма ее записи должна быть строго повторена в конспекте ученика, если он пользуется своими записями, а не вашими распечатками к уроку) разбираем по смыслу построчно, и так же заучиваем наизусть.
5. Обсуждение, как выполняется закон на различных примерах:
- условие покоя. Если условие покоя такое же как для равномерного прямолинейного движения, откуда тело знает, что ему делать, двигаться равномерно или покоиться? Роль начальных условий;
- хоккеист, шайба. Относительность покоя;
- нужна ли телеге лошадь для равномерного движения? Трение.
На следующем уроке после еще одного разбора (опроса по теме) для закрепления решаем качественные задачи (дискутируем) на проявление I закона Ньютона, в том числе с подвохами и хитринками. Задача (не слишком простая) -
сломать бытовые представления о причинах покоя или равномерного движения, утвердить формулировку I закона Ньютона в качестве
закона, приучить
пользоваться законом при упоминании слов «покой» или «равномерное движение» (то есть снова
дедуктивное мышление).
Один из способов слома – освоение использования ребенком научной терминологии, уход от бытового языка. А для этого заучивание материала с привычными для данной науки оборотами речи, терминами и пр. Между тем для понимания необходимо будет каждому выстроить мост между научным и бытовым пониманием.
Ниспровержение утверждения Аристотеля (и ему подобных): "Если на тело не действуют никакие силы, тело всегда находится в покое."
Добейтесь, чтобы дети перестали верить аристотелевым утвердениям. В противном случае урок пройдет мимо, и вы будете вынуждены беспомощно и бесполезно призывать к использованию закона, а дети и дальше будут пользоваться бытовыми представлениями, даже зная формулировку I закона Ньютона!
Пример III. Вывод формулы давления газа. Основное уравнение МКТ идеального газа.
Длинный и не простой, но очень полезный в научном плане вывод формулы давления газа. По сути это классное продолжение (развитие) дискуссии о молекулах. Только теперь в количественном отношении, а это не просто слова, это можно будет измерить! Это уже будет стопроцентное доказательство дискретности вещества!
Большой торт, правильно, едим по кусочкам. Наш план таков.
1. Идеальный газ, как модель реального. Реальный газ, как сущее.
2. Факт: газы всегда производят давление на стенки сосуда и окружающие их тела.

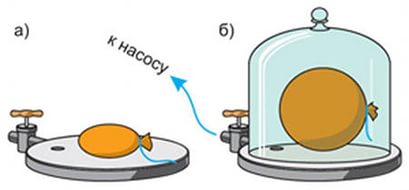
а) Давление: p = F/S (1).
Предположим, что
давление газа есть результат ударов его многочисленных молекул. Модель давления газа: желоб с горошинами.
Исходя из этих представлений, попробуем
вывести формулу давления газа и покажем, что она
выполняется. Это будет серьезным теоретическим достижением!
Мы ученикам: следите внимательно!
б) В формуле (1) F – сила удара молекул за небольшое время ∆t, а S – площадь поршня в сосуде. Если f
ср – средняя сила удара одной молекулы, а z – число ударов этих молекул, то F = zf
ср. Все пока просто: надо найти этих два числа z и f
ср и поделить их произведение на площадь поршня, и всё!
Займемся числом ударов, а потом средней силой удара молекул.
Найдем, сколько молекул успеют стукнутся о поршень за время ∆t. За это время до поршня успеют долететь только молекулы, которые к начальному времени расположены от поршня не далее расстояния CC’ = |v
x|
ср ∆t. Остальные не успеют.
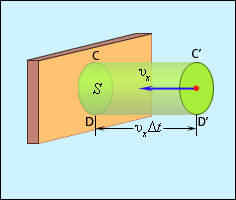
Число молекул, расположенных на этом расстоянии подсчитать тоже несложно: N = n V
CC’DD’, где
V
CC’DD’ = |CC’|S = |v
x|
ср ·∆
t·S.
Учитывая, что в сторону поршня летит в среднем лишь половина молекул (а другая от поршня), получим: z = N/2 = n·|v
x|
ср ·∆t·S/2. (2)
Ура! Одного нашли!
в) Молекула массой m
0 ударяется в поршень и отлетает. Мы такую задачу решали через закон сохранения импульса. В проекции на ось х: f·∆t = m
0v
x – m
0v
0x. Но при упругом ударе v
x = v
0x. Поэтому (с учетом знаков проекций): f·∆t = 2m
0|v
x| или f
ср = 2m
0|v
x |
ср/∆t. (3)
Важно: |v
x|
ср, v
x ср, и |v
x ср| не одно и тоже. Последние два равняются нулю, ибо в среднем молекулы остаются на месте (цилиндр с молекулами никуда не едет!). Усреднять имеет смысл именно |v
x|.
Итак, нашли второго.
г) Собираем в кучу всё, что нашли (в формулу (1) вставляем формулы (2) и (3)):
p = (n·|v
x|
ср·∆t·S/2)· (2m
0|v
x ср /∆t)/S = nm
0v
x 2ср. (4)
Модульные скобки можно опустить, так как возведение в четную степень по любому даст положительное число.
Это очень всё хорошо, ибо две величины из трех нам хорошо известны, как концентрация молекул и масса молекулы. Остается только более удобно записать v
x2ср, лучше это сделать через v
2ср. Здесь может быть удобно быстро вспомнить о том, насколько велики или малы встречающиеся нам величины: концентрация молекул газа n, масса молекулы m
0, средняя скорость молекул газа v
ср, средняя сила удара молекулы f
ср, число ударов молекул в поршень z.
д) Как в учебнике выводим v
x2ср =
1/
3v
2ср. Но только у нас ребенку понятно, зачем мы лезем в эти дебри с проекциями и скоростями молекул, а в учебнике нет!
е) Подставляем в формулу (4): p =
1/
3nm
0v
ср 2. (5) – Основное уравнение МКТ ИГ.
Заметим симпатичную парочку (!): m
0v
ср 2 = 2E
ср.
Получаем еще одну полезную формулу: : p =
2/
3nЕ
ср. (6)
Еще одна симпатичная парочка: nm
0 = m
0N/V = m/V = ρ. Значит: p =
1/
3·ρ·v
ср 2. (7)
Целое соцветие полезных формул!
Добавляем цитаты из учебника: Формулы (5), (6) и (7) связывают макроскопическую величину – давление р, которое может быть измерено манометром, - с микроскопическими и является мостом между двумя мирами: макро и микроскопическим. Формулу (5) легко проверить на опыте, и подтвердить, что не только давление газа – действительно результат ударов молекул, но и что сами газы состоят из этих самых молекул, то есть не являются сплошными телами.
Не забываем выразить свое восхищение красотой полученного результата! Столь витиеватый путь привел нас к компактным, простым и понятным формулам, а ведь мы начинали лишь с одного предположения: давление газа – результат ударов молекул. И всё!
Заучить вывод формул можно только по маленьким частям. На следующем уроке - кто больше пунктиков от «а» до «е» освоил. Мы же не будем требовать от всех всё? Сделай то, что можешь, но с доброй совестью.
А надо ли вообще заучивать этого монстра? Заученный и понятый вывод формулы, обладает свойством убедительности и доказательности, а услышанный – нет!
***
Приведенные здесь примеры должны были показать, как препарируя логическую нить доказательств и выводов, используемых на уроке теоретических знаний, мы приучаем детей к владению языком физической науки (терминологии), строгости доказательств, способам рассуждений и подходам, характерным для физики, в решении вопросов, возникающих в ходе теоретических исследований, двигаясь с известным усилием от бытового мышления к научному.
Приложение 1.
Дискуссия на тему «Строение вещества».
Шикарную дискуссию нам удавалось организовать в начале седьмого класса. Особая польза от нее заключалась еще и в том, что учитель становился на сторону противников атомистов, оставляя ученикам защищать атомистскую теорию. Иногда мы условно рядились в вымышленные образы Демокрита и, к примеру, Фомы Аквинского. Хотя жили они в совершенно разных эпохах, это не мешало нашей дискуссии, ибо герои условны.
Мы сообщали на уроках основные положения молекулярной теории строения вещества, но как сугубое мнение атомистов, то есть не бесспорное. А затем учиняли этим атомистам полный разгром, заимствовав аргументы из древнегреческих источников.
Самый сложный вопрос для семиклассников – вопрос о пустоте, о том, что между молекулами. Пустота это ничто, или нечто? Древние умели формулировать красиво. Надо сознаться в том, что мы были грешны перед строгой наукой в том, что не давали окончательных ответов на самые глубокие вопросы, руководствуясь тем, что вопросы важнее решений. Мы говорили, если между молекулами ничего нет, значит и нет промежутков между ними, а значит вещество должно быть сплошным! А если между молекулами что-то есть, то оно должно состоять из молекул, молекула к молекуле – опять вещество сплошное! Нет никаких молекул! Дело часто доходило до визгов и криков, настолько сильными были интеллектуальные потрясения моих школьников. Очень интересно, к каким приемам прибегают ученики, когда кончаются аргументы. Надо быть готовым и к этому.
Проще им было с силами взаимодействия между молекулами. Если есть силы отталкивания, то почему все молекулы не разбежались друг от друга в дальние концы Вселенной?
Если есть силы притяжения между молекулами, то почему они не слиплись в один сплошной комок? Если молекулы движутся, то почему они не разбежались? И т.д. и т.п…
Правильно разыгранные роли содействовали выходу дискуссии далеко за пределы не только урока, но и класса, и школы в виде споров с родителями и знакомыми.
Заняв заранее проигрышную позицию, но проявляя упорство, мы порождаем в детях упорство не меньшей силы, но в чем? В том, что они отстаивают научные истины! Что может быть полезнее? При этом мы учим их вести дискуссию по правилам культурного диалога. Мы иногда говорим, так нельзя, это запрещенный прием. Ибо культура начинается с табу.
Дискуссия, неизменно содержащая в себе противопоставление – одно из мощных средств против клипового сознания. Она рождает в детях ощущение связанности мира.
Второе, что дает дискуссия (особенно не завершенная), повторные возвраты к теме, в том числе и через достаточные временные отрезки (в нашем случае понятие поля в электродинамике, теория близкодействия к разговору о «пустом» пространстве, а затем в ядерной физике элементарных частиц – «не пустая» пустота, рождающая потоки частиц из «ничего» при столкновении гамма-квантов). Эти возвраты рождают глубину понимания, которой так не хватает нашей молодежи. Разве мы в этом не правы?
Другие темы для диксуссий:
- Апории Зенона.
- Невозможность ускорения абсолютно твердого тела.
- Степень реальности тепловой "смерти" Вселенной.
- Парадос Декарта.Детерминизм Вселенной.
- Свет - волна или поток частиц?
- Электрон - частица или волна?
- Как работатет зеленый (или синий) полупроводниковый лазер, которого не может быть в природе? Как "покрасить" свет в другой цвет?
и т.д.